Math Made Easy: Problem of the Day 127

Many geometry problems can be solved with subtraction of areas. The technique is useful enough that it’s very popular on standardized tests. The SAT, ACT, and GRE all present problems that are best solved using this technique. The situation I present today is no different.

We cannot use the regular polygons formula to calculate the area of the octagon, as it is not quite a regular triangle. Since the exterior line segments of our drawing are all equal,, and four sides of the octagon are the hypotenuses of the four triangles, those sides are NOT congruent to the legs of the triangles. Four of the sides of the octagon ARE congruent to the legs of those triangles. That means that those four sides are not congruent to the four sides that are hypotenuses. So we must use subtraction of areas to find the area of our octagon. Let’s first redraw it without the colours.

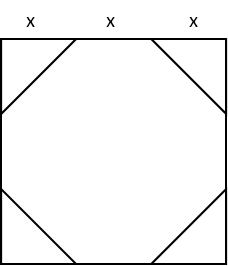
Looking at the drawing, we can readily see that the area of the octagon will be equal the area of the square less the area of the four triangles. Like this:

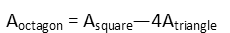
So we remind ourselves of the formula for the area of the square, the simplest of all area formulae:

Each side of the square is three x’s, so we plug that in:

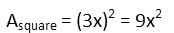
Now to remind ourselves of the formula for the area of a triangle.

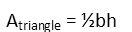
The base and height of each triangle are the same, x, so that gives us:

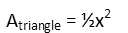
And now we just plug in the area we found for the square and triangles into the equation we wrote for the area of the octagon.

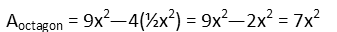
Now that we have the area of the octagon, we review our question to check what we were asked. It wants the portion of the area of the square that the octagon’s area is, so we just make a fraction with the octagon’s area on top and the square’s on the bottom. We simplify it, and if we like, we can convert that into a percentage (on a standardized test, check the answers to see what format they want – it could be a fraction, percentage, or even a decimal).

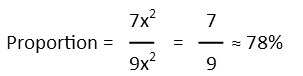
And, there we go! No complicated math needed. If you could do this problem on your own, you’d be ready for the Graduate Record Exam.