Math Made Easy: Problem of the Day 29

Our painter needs help with a new logo. Can you help him to decide how much paint he needs to buy this time?

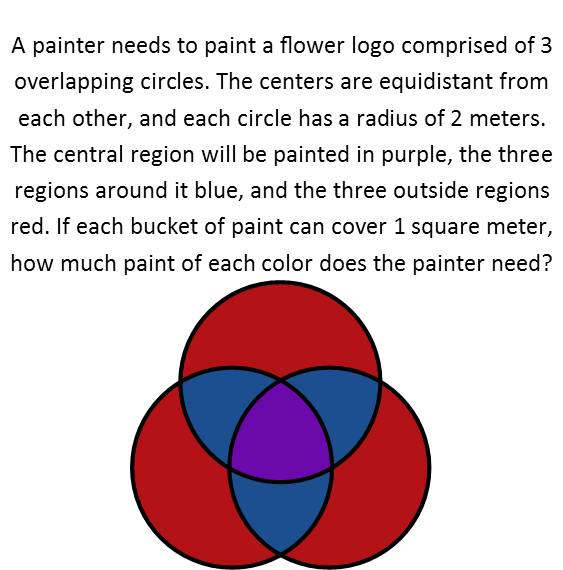
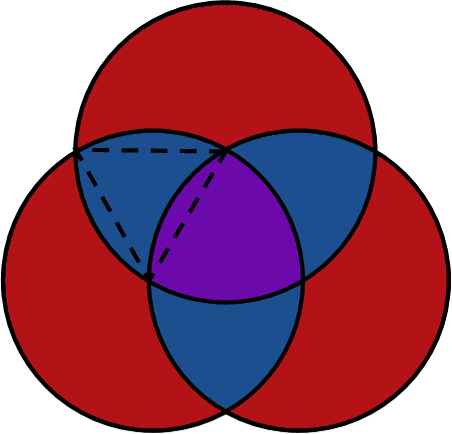
Now don’t let this one intimidate you! It’s easier than it looks! We must recognize that this problem is all about geometry. And specifically, it’s about triangles and circles. Don’t see any triangles? That’s okay, they’re actually there. So, like with any hard problem, let’s break this down into pieces so we can tackle one at a time.

We’ll do the purple area first. Since all three circles are identical, and their centers are equidistant, then there is actually a triangle formed by their points of intersection. The purple area contains that triangle, so each of the points of the purple area are the vertices of the triangle. This means the area of the purple region is equal to the area of the triangle plus the area of each of those slivers. And we know the general formula for the area of any triangle.

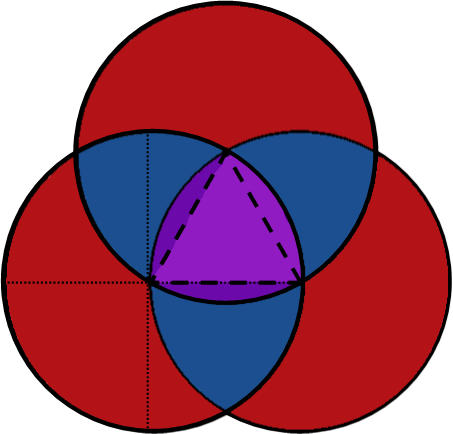
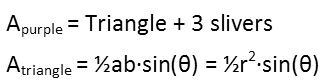
Each of the slivers is exactly the same area as the others. But how do we get the area of each sliver? That’s actually pretty simple – see how in the picture, I’ve lightened the arc sector that is defined by one of the angles of the triangle. Do you see how the sliver and the triangle are both part of that? Well, if you find the area of the arc sector, which is just a fraction of the area of the circle, you can find the area of the sliver by subtracting the triangle’s area from the arc sector’s, like so (we find the fraction of the circle by dividing the arc sector’s measure in radians by the measure of an entire circle in radians):

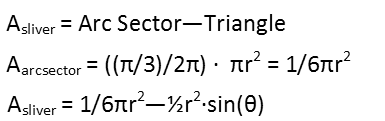
So now we just add those together (I’m just going to multiply the sliver times three instead of writing three of it), and then plug in our radius of 2, as well as our angle, and solve. The angle is π/3 (60 degrees) because the triangle is an equilateral triangle – its sides are the radii of the circle, so all of them are the same, so all its angles are congruent.

That comes out to about 4.28, so our painters needs 5 buckets of purple paint (since he can’t buy a partial bucket of paint).

We’ve actually done most of the hard work now. When we examine the blue areas, we can see they are almost the same as the purple area, with one little difference. While their points are defined by the same triangle, and they therefor have the same slivers, instead of all three slivers being added to the triangle, we can see that two are being added, while one is being subtracted (it cuts into the triangle instead of bulging out from it). So we can use the work we’ve done before to help us come up with our equation for the area of the blue regions (note the whole thing is multiplied by 3 since there are three blue regions):

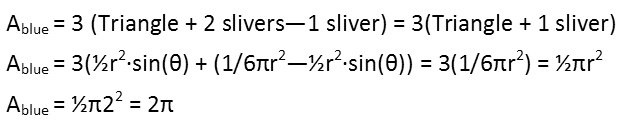
This comes out to a little over 6.28, so our painter needs to buy 7 buckets of blue paint.

Finally, the red area. We’ve actually practically done all our work by now. Hopefully by now you can see that the red area is just the area of all three circles minus the total blue area and purple area. So we have this for the red area:

That comes out to about 27.13, so our painter needs to buy 28 buckets of red paint.

By breaking this down, and envisioning the triangle formed by the circles’ intersections, we were able to take what looked like an incredibly difficult problem, and actually made it fairly simple. We helped our painted to determine he needs 5 buckets of purple paint, 7 of blue, and 28 buckets of red. Without doing the math ahead of time, one most probably would have purchased too many of one color, and too few of another. It helps to know your mathematics!