Math Made Easy: Problem of the Day 9

Let’s do some complex numbers today. That is, those numbers with a real and an imaginary component. I’m not going to phrase this one in real world terms, though there are definitely many real world applications that involve complex numbers, such as light and electronics.

Here’s your problem. Try to solve it without looking at the solution.

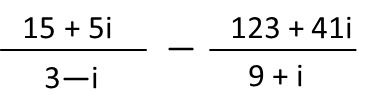
Okay, and now for your solution.

Since we’re adding two fractions, normally we’d try to find a common denominator so that we can do so. But let’s not do that just yet. I find that, with complex numbers, you’re shooting yourself in the foot if you try to add the fractions BEFORE you rationalize them. That is the process of getting any radicals or imaginary numbers out of the denominator, or bottom, of the fraction. With this particular problem, I’m going to rationalize them each separately, treating them like separate problems until I’ve rationalized both fractions.

For the first one, I see that the numerator has a common factor of 5 in both terms, so I’ll factor that out. To rationalize a fraction with a complex number in the denominator, you multiply it by that version of 1 that is made up of its complex conjugate. That is whatever you need to multiply it by to get a real number, and is easily found simply by just changing the sign of the complex number. So we’re going to multiply this fraction by (3+i)/(3+i). Using foil, just like in normal algebra, since we’re not going to let that little “i” throw us, we expand the products, and then add like terms until we get to the simplest form of the fraction, remembering that, since i is just √-1, then i²=-1. Though in the steps below I didn’t *quite* simplify it all the way. I’ll do the final simplification when I put both fractions back together to add them.

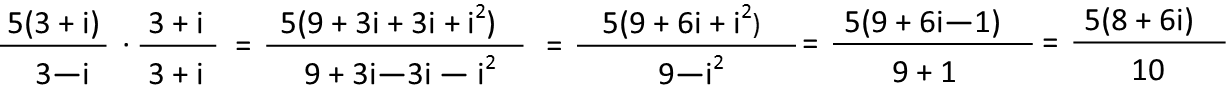
For the second one, I see the numerator has a common factor of 41, and I factor it out. Then I follow the same step of multiplying by the complex conjugate of the denominator over itself, foil the products, and simplify.

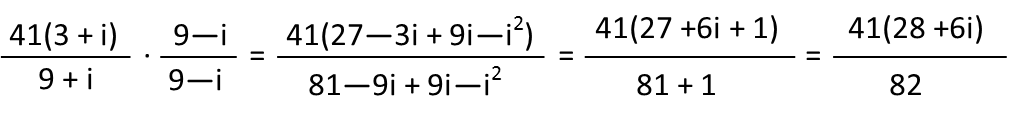
Now I’m going to put both fractions back together. The reason I didn’t simplify the coefficient of the numerator and denominator before was for this step. Sometimes, with adding complex fractions like this, doing so actually shoots you in the foot, because you may have to just multiply again to get a common denominator. Happily, with this one I can see that both fractions simplify to have a denominator of 2 and no coefficient in the numerator. So I simplify them, combine the numerators as one numerator over the common denominator of 2, and simplify. Turns out that big ugly thing we started with is just simply -10.

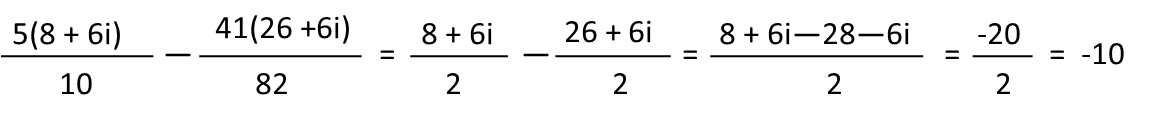
The lesson for today is this: don’t go on math autopilot (it’s a common lesson). If we’d gone straight to common denominators, this problem would have been a nightmare. Rationalizing and simplifying the fractions first, saving the final simplification of the coefficients for the last step, made the problem much, much easier.