Math Made Easy: Problem of the Day 94

A parallelepiped is basically a three dimensional version of a parallelogram. All its sides are parallel to an opposing side. Each edge is parallel to another edge. Because of this, all you need to define a parallelepiped is three edges, which we can describe as vectors. And one of the beauties of vector calculus, is using just those three edges, we can do such nifty things as finding out how much volume that shape has without having to do a bunch of geometric acrobatics. Which we could do, if we wanted to spend the next four hours trying to work on this problem. Or we can take advantage of some of the basic operations in vector calculus to help us out here.

I’m going to do the latter. To find the volume of the figure formed by three vectors, we take dot product of one of them with the cross product of the other two. This will give us a scalar, which is our desired result for a volume.

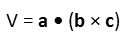
So, plugging our vectors into that, we start with:

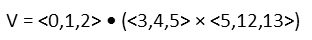
To resolve this, just as in scalar mathematics, we start with the junk inside the parenthesis first. So let’s take the cross product of those two vectors. We haven’t done in any of our problems of the day, so here’s how we do it. It’s not as hard as some texts make it look at first. Think of it visually, and it should be pretty easy. When we find a cross product, we should get another vector. Each component of that vector is determined by the components of the original vectors that DO NOT correspond to the component you’re currently working on. So, if you’re working on the x component, it’s made up of the y and z components of the original vectors. For the x component, you take the product of the first vector’s y and the second vector’s z and subtract the product of the second vector’s y and the first vector’sz, making a kind of cross, like below:

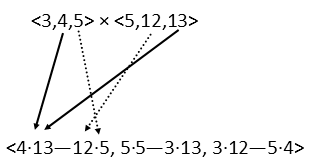
For the y components, you switch it up. We find that component by finding the product of the second vector’s x and the first vector’s z and subtract the product of the first vector’s x and the second vector’s z, like below:

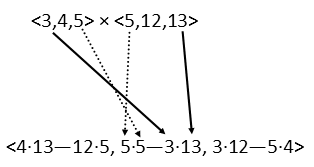
The z component is done just like the x component, but with the x’s and y’s of the original vectors.

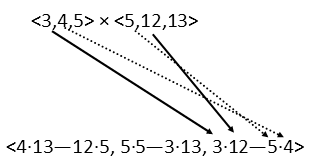
So, finding the cross product of our vectors in the parentheses, we get:

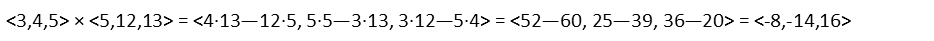
Now we just need to take the dot product of our first vector and the resulting cross vector that we just found. Remember we talked about how to find a dot product in Problem of the Day 92. We just add the products of like components:

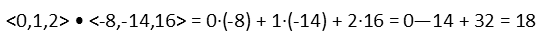
And we see the volume of our parallelepiped is 18 cubic units.

If you like, you can try to figure out a geometric method that doesn’t involve vector calculus. It might take you some time.